Implied volatility helps us understand the extent of positive or negative movement that the market participants are expecting in coming days. It tells us only about the extent of the move and not regarding the direction. Implied volatility is forward looking unlike historical volatility. Implied volatility plays a role in options pricing.It is a measure of risk.
What is Implied Volatility?

In simple terms, Implied volatility is “The market’s current forecast of future volatility”. Historical volatility is calculated based on historical price changes while Implied Volatility is calculated based on the current prices of options contracts. This means, if there are no options contracts for a particular instrument, there will not be any implied volatility information for that instrument.
How do we calculate Implied Volatility?

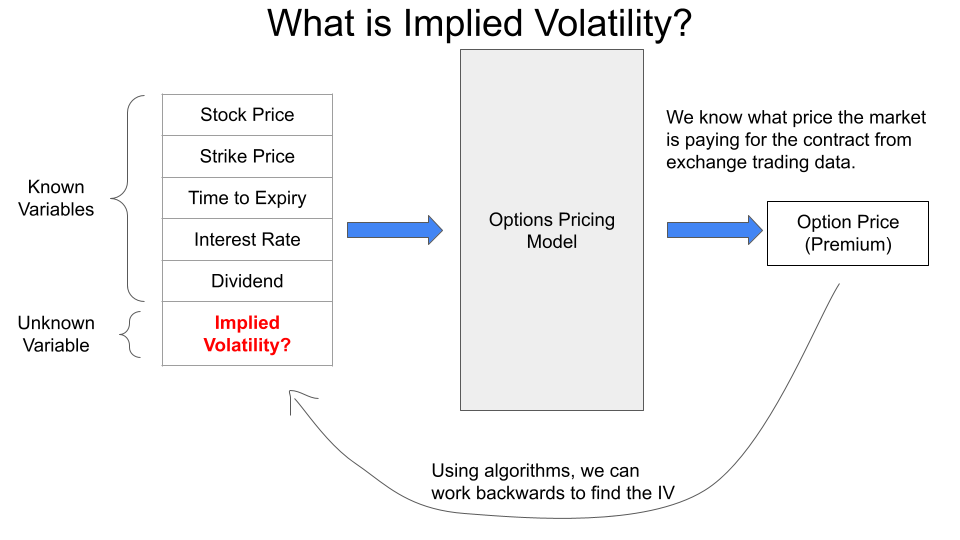
A typical options pricing model takes the inputs mentioned on the left side side of the above diagram and generates a theoretical value of the options contract. As you can see, out of the six variables, five of them are variables which are easily known. Implied Volatility has to be estimated to calculate the options price.
To know the Implied Volatility estimated by the market, we can work backwards. Options Price that the market is ready to pay is already known from the exchange data on your broker platform. We also know the other five variables. So we can solve for the one unknown variable i.e Implied Volatility using certain algorithms.
How does option premium change with change in Implied Volatility?
Vega is part of Options Greeks that establishes the relationship for change in options premium with change in Implied Volatility. If the volatility of the underlying changes by 1%, the price of the option will change by ‘Vega’ amount.


We can calculate the value of Vega and other Greeks also using the Options Pricing Model such as the Black-Scholes pricing model.
Will Implied Volatility have same impact on all options premiums?
In terms of points, you will see a greater impact on at-the-money contracts as compared to in the money or out of the money strikes.
In percentage terms, you will see a greater impact on out-of-the-money contracts as compared to in-the-money or at-the-money contracts.
You will see a greater impact on contracts having a longer time to expiry.

The above table shows is an example of how change in IV differently impacts different strike prices. As we can see, the OTM strike changed by 16%, ATM by 6.28% and the ITM by 2.13%. It is noteworthy that ATM has the highest Points change.
What is India VIX
India VIX is a volatility index based on the index option prices of NIFTY index. The NSE calculates India VIX using the Nifty Options order book for current and near month expiries. India VIX indicates the expected market volatility over the next 30 calendar days in annualised form.
Strategy Example 1

Long Straddle Characteristics:
Gamma = + (Positive)
Positive gamma indicates that the delta of a position moves in the same direction as the change in underlying stock’s price. The net delta of a long straddle gets increasingly positive as the stock price rises and increasingly negative if stock falls. The position will benefit from Sharp movement in underlying.
Vega = + (Positive)
The value of position increases with increase in Implied Volatility.
Theta = – (Negative)
The value of position decreases with the passage of time.
From the above characteristics, it is evident that the position benefits from increase in Volatility due to positive Vega. It also benefits from a sharp movement in the stock, either up or down due to positive gamma. The position will have negative impact due to negative theta. To avoid theta decay, we will not carry the position overnight. To benefit from positive Vega, we will enter when we anticipate that the volatility will increase.
We are not taking position on Thursday to avoid sharp theta decay on expiry as we have created the strategy on weekly options.
Long Straddle = One long call and One long put on the same underlying, strike and expiry.
Scanner Example 1
This scanner scans for contracts where IV has suddenly shot up.

Strategy Example 2

Short Straddle = One short call and One short put on the same underlying, strike and expiry.
Short Straddle Characteristics:
Gamma = – (Negative)
Negative gamma indicates that the delta of a position moves in the opposite direction of the underlying stock’s price change. The net delta of a short straddle becomes increasingly negative as the stock price rises and and net delta becomes increasingly positive as the stock falls. Sharp movement in underlying will negatively impact the position.
Vega = – (Negative)
The value of position increases with decrease in Implied Volatility.
Theta = + (Positive)
The value of position increases with the passage of time.
From the above characteristics, it is evident that the position benefits from decrease in Volatility due to negative Vega. It also benefits from a sharp movement in the stock, either up or down is detrimental for the position. The position will have positive impact due to positive theta of the position as we are short on both the contracts. To benefit from negative Vega, we will enter when we anticipate that the volatility will decrease.
Scanner Example 2
This scanner scans for contracts where Vega is between 10 and 15.

Conclusion
- Implied volatility helps us understand the extent of positive or negative movement that the market participants are expecting in coming days.
- Vega helps us determine the change in Options Premiums based on changes in IV.
- IV Impacts different strike prices differently.
- India VIX indicates the expected market volatility over the next 30 calendar days and is based on the index option prices of NIFTY index.
- We can create and backtest strategies based on Implied Volatility on Streak.
- We can be optimise the conditions to find increasing/decreasing IV to improve strategy performance.
Disclaimer: The information provided is solely for educational purposes and does not constitute a recommendation to buy, sell, or otherwise deal in investments.










Pingback: Trading with Greeks on Streak - Part 2 (Theta Decay & Time Value) - Streak Tech